So I have a secret project. Come closer. I’m developing an R package that implements Bayesian alternatives to the most commonly used statistical tests. Yes you heard me, soon your t.testing days might be over! The package aims at being as easy as possible to pick up and use, especially if you are already used to the classical .test functions. The main gimmick is that the Bayesian alternatives will have the same calling semantics as the corresponding classical test functions save for the addition of bayes. to the beginning of the function name. Going from a classical test to the Bayesian version will be as easy as going from t.test(x1, x2, paired=T) to bayes.t.test(x1, x2, paired=T).
The package does not aim at being some general framework for Bayesian inference or a comprehensive collection of Bayesian models. This package should be seen more as a quick fix; a first aid for people who want to try out the Bayesian alternative. That is why I call the package Bayesian First Aid.

Why Bayesian First Aid?
To paraphrase John D. Cook paraphrasing Anthony O’Hagan: The great benefit with Bayesian inference is that it is a principled and coherent framework with to produce inferences that have a (relatively) straight forward interpretation (it’s all probability). Furthermore, once you’ve got the Bayesian machinery going you have great flexibility when it comes to modeling your data.
This flexibility is a great thing and stands in contrast with how classical statistics is presented; as a collection of prepackaged routines that you can select from but not tinker with. Just pick up any psychology statistics textbook (like me, me or me) and you will find the same canonical list: Binomial test, one sample t-test, two samples t-test, correlation test, chi-square test, etc. In Bayesian statistics you can quickly escape the cookbook solutions, once you get a hang of the basics you are free to tinker with distributional assumptions and functional relationships. In some way, classical statistics (as it is usually presented) is a bit like Playmobile, everything is ready out of the box but if the box contained a house there is no way you’re going to turn that into a pirate ship. Bayesian statistics is more like Lego, once you learn how to stick the blocks together the sky is the limit.

However, cookbook solutions (recipes?) have some benefits. For one thing, they are often solutions to commonly encountered situations, otherwise there wouldn’t be a need for a prepackaged solution in the first place. They are also easy to get started with, just follow the recipe. In R the statistical cookbook solutions are really easy to use, due to all the handy *.test function many classical analyses are one-liners.
A Bayesian analysis is more difficult to pull off in one line of R and often requires a decent amount of work to get going. The goal of Bayesian First Aid is now to bring in some of the benefits of cookbook solutions and make it easy to start doing Bayesian data analysis. The target audience is people that are curious about Bayesian statistics, that perhaps have some experience with classical statistics and that would want to see what reasonable Bayesian alternatives would be to their favorite statistical tests. For sure, it is good to have a firm understanding of the math and algorithms behind Bayesian inference but sometimes I wish it was as easy to summon a posterior distribution as it is to conjure up a p-value. Easy summoning of posterior distributions would be useful, for example, if you want to try teaching Bayesian stats backwards.
Bayesian First Aid Design Rationale
Bayesian First Aid is foremost inspired by John Kruschke’s Bayesian Estimation Supresedes the T-test (BEST) and the related BEST R package. BEST can be used to analyze data you would classically run a t-test on, but it does not have the same distributional assumptions as the t-test, and what more, it isn’t even a test! Both these differences are a Good Thing™. Instead of assuming that the data is normally distributed BEST assumes a t distribution which, akin to the normal distribution, is symmetric and heap shaped but, unlike the normal distribution, has heavy tails and is therefore relatively robust against outliers. Bayesian First Aid is going for the same approach, that is, similar distributional assumptions as the classical tests but using more robust/flexible distributions when appropriate.
BEST is neither a statistical test in the strict sense as there is no testing against a point null going on. Instead of probing the question whether the mean difference between two groups is zero or not BEST does parameter estimation, effectively probing how large a difference there is. The question of how large or how much is often the more sensible question to ask, to learn that pill A is better than pill B actually tells you very little. What you want to know is how much better pill A is. Check out The Cult of Statistical Significance (both a book and a paper) by Ziliak and McCloskey to convince yourself that parameter estimation is what you really want to do most of the time rather that hypothesis testing. As in BEST, the Bayesian First Aid alternatives to the classical tests will be parameter estimation procedures and not point null tests.
The main gimmick of Bayesian First Aid is that the Bayesian version will have almost the same calling semantics as the corresponding classical test function. To invoke the Bayesian version just prepend bayes. (as in BAYesian EStimation) to the beginning of the function, for example, binom.test becomes bayes.binom.test, cor.test becomes bayes.cor.test and so on. The Bayesian version will try to honor the arguments of the classical test function as far as possible. The following runs a binomial test with a null of 0.75 and an 80 % confidence interval: binom.test(deaths, total_ninjas, p=0.75, conf.level=0.8). The Bayesian version would be called like bayes.binom.test(deaths, total_ninjas, p=0.75, conf.level=0.8) where p=0.75 will be interpreted as a relative frequency of special interest and the resulting report will include the probability that the underlying relative frequency of ninja casualties go below / exceed 0.75. conf.level=0.8 will be used to set the limits of the reported credible interval.
A defining feature of Bayesian data analysis is that you have to specify a prior distribution over the parameters in the model. The default priors in Bayesian First Aid will try to be reasonably objective (if you believe it is silly to call a Bayesian analysis “objective” James Berger gives many god arguments for objective Bayes
here). There will be no way of changing the default priors (ghasp!). We only try to give first aid here, not the full medical treatment. Instead it should be easy to start tinkering with the models underlying Bayesian First Aid. The generic function model.code takes a Bayesian First Aid object and prints out the underlying model which is ready to be copy-n-pasted into an R script and tinkered with from there. All models will be implemented using the
JAGS modeling language and called from R using the
rjags package. In addition to model.code all Bayesian First Aid objects will be plotable and summaryiseable. A call to diagnostics will show some MCMC diagnostics (even if this shouldn’t be necessary to look at for the simple models). For an example of how this would work, see the sneak peek further down.
Base R includes many statistical tests some well known such as cor.test and some more unknown such as the
mantelhaen.test. The classical tests I plan to implement reasonable Bayesian alternatives to are to begin with:
- binom.test
- t.test
- var.test
- cor.test
- poisson.test
- prop.test
- chisq.test
- oneway.test
- lm (not really a test but…)
- ???
- PROFIT!
The development of Bayesian First Aid can be tracked on GitHub but currently the package is far from being usable in any way. So don’t fork me on GitHub just yet…
I’m grateful for any ideas and suggestion regarding this project. I’m currently struggling to find reasonable Bayesian estimation alternatives to the classical tests so if you have any ideas what to do with, for example, the chisq.test please let me know.
A Sneak Peak at Bayesian First Aid
Just a quick look at how Bayesian First Aid would work. The following simple problem is from a statistical methods course (since publishing this post the page for that statistics course has unfortunately been removed):
A college dormitory recently sponsored a taste comparison between two major soft drinks. Of the 64 students who participated, 39 selected brand A, and only 25 selected brand B. Do these data indicate a significant preference?
This problem is written in order to be tested by a binomial test, so let’s do that:
binom.test(c(39, 25))
Exact binomial test
data: c(39, 25)
number of successes = 39, number of trials = 64, p-value = 0.1034
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.4793 0.7290
sample estimates:
probability of success
0.6094
Bummer, seems like there is no statistically significant difference between the two brands. Now we’re going to run a Bayesian alternative simply by prepending bayes. to our function call:
library(BayesianFirstAid)
bayes.binom.test(c(39, 25))
Bayesian first aid binomial test
data: c(39, 25)
number of successes = 39, number of trials = 64
Estimated relative frequency of success:
0.606
95% credible interval:
0.492 0.727
The relative frequency of success is more than 0.5 by a probability of 0.959
and less than 0.5 by a probability of 0.041
Great, we just estimated the relative frequency of choosing brand A assuming the following model:
In this simple example the estimates from binom.test and bayes.binom.test are close to identical. Still we get to know that The relative frequency of success is more than 0.5 by a probability of 0.956 which indicates that brand A might be more popular. At the end of the day we are not that interested in whether brand A is more popular that brand B but rather how much more popular brand A is. This is easier to see if we look at the posterior distribution of :
plot(bayes.binom.test(c(39, 25)))
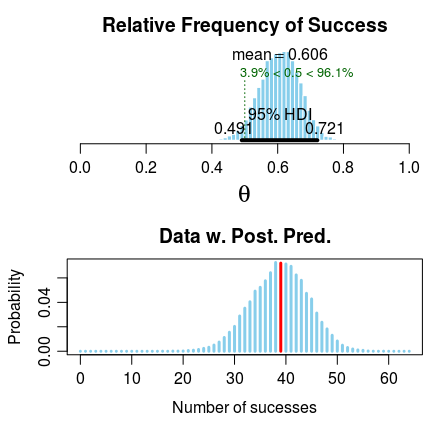
So it seems that brand A might be more popular than brand B but not by too much as the posterior has most of its mass at a relative frequency between 0.5 and 0.7. The college cafeteria should probably keep both brands in stock if possible. If they need to choose one brand, pick A.
Perhaps you want to tinker with the model above, maybe you have some prior knowledge that you want to incorporate. By using the model.code function we get a nice printout of the model that we can copy-n-paste into an R script.
model.code(bayes.binom.test(c(39, 25)))
### Model code for the Bayesian First Aid alternative to the binomial test ###
require(rjags)
# Setting up the data
x <- 39
n <- 64
# The model string written in the JAGS language
model_string <-"model {
x ~ dbinom(theta, n)
theta ~ dbeta(1, 1)
x_pred ~ dbinom(theta, n)
}"
# Running the model
model <- jags.model(textConnection(model_string), data = list(x = x, n = n),
n.chains = 3, n.adapt=1000)
samples <- coda.samples(model, c("theta", "x_pred"), n.iter=5000)
#Inspecting the posterior
plot(samples)
summary(samples)