Hello stranger, and welcome! 👋😊
I'm Rasmus Bååth, data scientist, engineering manager, father, husband, tinkerer,
tweaker, coffee brewer, tea steeper, and, occasionally, publisher of stuff I find
interesting down below👇
Christmas is soon upon us and here are some gift ideas for your statistically inclined friends (or perhaps for you to put on your own wish list). If you have other suggestions please leave a comment! :)
1. Games of probability
A recently released game where probability takes the main role is
Pairs, an easy going press-your-luck game that can be played in 10 minutes. It uses a custom “triangular” deck of cards (1x1, 2x2, 3x3, …, 10x10) and is a lot of fun to play, highly recommended!

Another good gift would be a pound of assorted dice together with the seminal Dice Games Properly Explained by Reiner Knizia. While perhaps not a game, a cool gift to someone that already has a pound of dice would be a set of
Non transitive Grime dice.
On the 21st of February, 2015, my wife had not had her period for 33 days, and as we were trying to conceive, this was good news! An average period is around a month, and if you are a couple trying to go triple, then a missing period is a good sign something is going on. But at 33 days, this was not yet a missing period, just a late one, so how good news was it? Pretty good, really good, or just meh?
To get at this I developed a simple Bayesian model that, given the number of days since your last period and your history of period onsets, calculates the probability that you are going to be pregnant this period cycle. In this post I will describe what data I used, the priors I used, the model assumptions, and how to fit it in R using importance sampling. And finally I show you why the result of the model really didn’t matter in the end. Also I’ll give you a handy script if you want to calculate this for yourself. :)
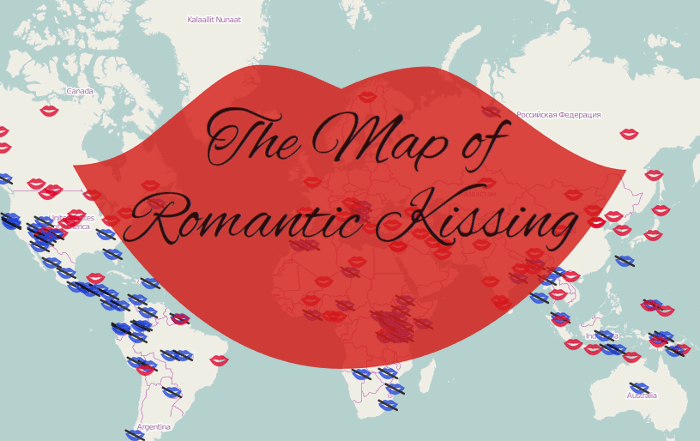
Romantic kissing is a cultural universal, right? Nope! At least not if you are to believe Jankowiak et al. (2015) who surveyed a large number of cultures and found that “sexual-romantic kissing” occurred in far from all of them. For some reasons the paper didn’t include a world map with these kissers and non-kissers plotted out. So, with the help of my colleague Andrey Anikin I’ve now made such a map using R and
the excellent leaflet package. Click on the image below to check it out:
The BASIC programming language was at one point the most widely spread programming language. Many home computers in the 80s came with BASIC (like the Commodore 64 and the Apple II), and in the 90s both DOS and Windows 95 included a copy of the
QBasic IDE. QBasic was also the first programming language I encountered (I used it to write a couple of really horrible text adventures). Now I haven’t programmed in BASIC for almost 20 years and I thought I would revisit this (from my current perspective) really weird language. As I spend a lot of time doing Bayesian data analysis, I though it would be interesting to see what a Bayesian analysis would look like if I only used the tool that I had 20 years ago, that is, BASIC.
This post walks through the implementation of the Metropolis-Hastings algorithm, a standard Markov chain Monte Carlo (MCMC) method that can be used to fit Bayesian models, in BASIC. I then use that to fit a Laplace distribution to the most adorable dataset that I could find: The number of wolf pups per den from a sample of 16 wold dens. Finally I summarize and plot the result, still using BASIC. So, the target audience of this post is the intersection of people that have programmed in BASIC and are into Bayesian computation. I’m sure you are out there. Let’s go!
This is a screencast of my
UseR! 2015 presentation: Tiny Data, Approximate Bayesian Computation and the Socks of Karl Broman. Based on
the original blog post it is a quick’n’dirty introduction to approximate Bayesian computation (and is also, in a sense, an introduction to Bayesian statistics in general). Here it is, if you have 15 minutes to spare:
A while back I wrote about
how the classical non-parametric bootstrap can be seen as a special case of the Bayesian bootstrap. Well, one difference between the two methods is that, while it is straightforward to roll a classical bootstrap in R, there is no easy way to do a Bayesian bootstrap. This post, in an attempt to change that, introduces a bayes_boot function that should make it pretty easy to do the Bayesian bootstrap for any statistic in R. If you just want a function you can copy-n-paste into R go to
The bayes_boot function below. Otherwise here is a quick example of how to use the function, followed by some details on the implementation.
Update: I’ve now created an R package that implements the Bayesian bootstrap, which I recommend instead of using the function described in this post. You can install it by running install.packages("bayesboot") in R and you can read more about it
here. The implementation is the same as here, but the interface is slightly different.
hygge
A Danish word (pronounced HU-guh) meaning social coziness. I.e. the feeling of a good social atmosphere. –
Urban Dictionary
Yes, there was plenty of hygge to go around this year’s UseR! that took place last week in Aalborg, Denmark. Everybody I’ve spoken with agrees that it was an extraordinary conference, from the interesting speakers and presentations to the flawless organization (spearheaded by
Torben Tvedebrink) and the warm weather. As there were many parallel session, I only managed to attend a fraction of the talks, but here are some of my highlights:
In
a previous post I used the
the Million Base 2.2 chess data base to calculate the predictive piece values of chess pieces. It worked out pretty well and here, just for fun, I thought I would check out what happens with the predictive piece values over the course of a chess game. In the previous analysis, the data (1,000,000 chess positions) was from all parts of the chess games. Here, instead, are the predictive piece values using only positions up to the 10th first full moves (a full move is when White and Black each have made a move):
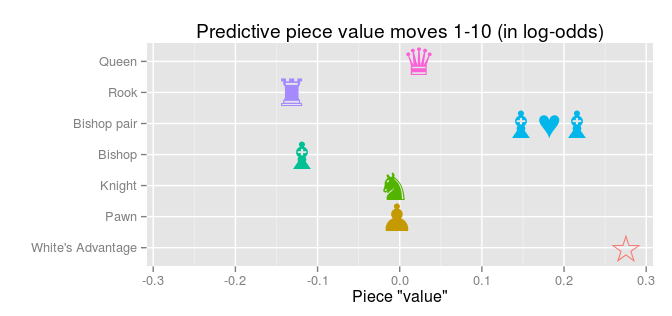
Who doesn’t like chess? Me! Sure, I like the idea of chess – intellectual masterminds battling each other using nothing but pure thought – the problem is that I tend to lose, probably because I don’t really know how to play well, and because I never practice. I do know one thing: How much the different pieces are worth, their point values:

This was among the first things I learned when I was taught chess by my father. Given these point values it should be as valuable to have a knight on the board as having three pawns, for example. So where do these values come from? The point values are not actually part of the rules for chess, but are rather just used as a guideline when trading pieces, and they seem to be based on the expert judgment of chess authorities. (According to the guardian of truth
there are many alternative valuations, all in the same ballpark as above.) As I recently learned that it is very important to be able to write Big Data on your CV, I decided to see if these point values could be retrieved using zero expert judgement in favor of huge amounts of chess game data.
The non-parametric bootstrap was my first love. I was lost in a muddy swamp of zs, ts and ps when I first saw her. Conceptually beautiful, simple to implement, easy to understand (I thought back then, at least). And when she whispered in my ear, “I make no assumptions regarding the underlying distribution”, I was in love. This love lasted roughly a year, but the more I learned about statistical modeling, especially the Bayesian kind, the more suspect I found the bootstrap. It is most often explained as a procedure, not a model, but what are you actually assuming when you “sample with replacement”? And what is the underlying model?
Still, the bootstrap produces something that looks very much like draws from a posterior and there are papers comparing the bootstrap to Bayesian models (for example,
Alfaro et al., 2003).
Some also wonder which alternative is more appropriate: Bayes or bootstrap? But these are not opposing alternatives, because the non-parametric bootstrap is a Bayesian model.
In this post I will show how the classical non-parametric bootstrap of
Efron (1979) can be viewed as a Bayesian model. I will start by introducing the so-called Bayesian bootstrap and then I will show three ways the classical bootstrap can be considered a special case of the Bayesian bootstrap. So basically this post is just a rehash of
Rubin’s The Bayesian Bootstrap from 1981. Some points before we start:
-
Just because the bootstrap is a Bayesian model doesn’t mean it’s not also a frequentist model. It’s just different points of view.
-
Just because it’s Bayesian doesn’t necessarily mean it’s any good. “We used a Bayesian model” is as much a quality assurance as “we used probability to calculate something”. However, writing out a statistical method as a Bayesian model can help you understand when that method could work well and how it can be made better (it sure helps me!).
-
Just because the bootstrap is sometimes presented as making almost no assumptions, doesn’t mean it does. Both the classical non-parametric bootstrap and the Bayesian bootstrap make very strong assumptions which can be pretty sensible and/or weird depending on the situation.




