I’ve dug up an old, never published, dataset that I collected back in 2013. This dataset fairly cleanly shows that it’s harder to remember words correctly if you also have to remember the case of the letters. That is, if the shown word is Banana and the subject recalls it as Banana, then it’s correct, but banana is as wrong as if the subject had recalled bapple. It’s not very surprising that it’s harder to correctly remember words when case matters, but the result and the dataset are fairly “clean”: Two groups, simple-to-understand experimental conditions, plenty of participants (200+), the data could even be analyzed with a t-test (but then please look at the confidence interval, and not the p-value!). So maybe a dataset that could be used when teaching statistics, who knows? Well, here it is, released by me to the public domain:

case-matters-memory-experiment.csv

In the rest of this post, I’ll explain what’s in this dataset and how it was collected, and I’ll end with a short example analysis of the data. First up, here’s how the memory task was presented to the participants (click here if you want to try it out yourself):

Why did I collect this data in the first place? For some reason, I wanted to “prove” that having to remember capitalization was hard in my UseR 2013 presentation The State of Naming Conventions in R. R is a bit incoherent in that it doesn’t follow any strict naming convention (you have NCOL, ncol, as.Date, Axis, etc.). But, to be honest, nowadays Rstudio auto-completion is so good that this doesn’t really matter anymore.

The word recall task

As you can see above, the task was a fairly standard free recall task where participants were shown a list of 12 words, one at a time, where each word was shown for two seconds. The participants were then asked to write down as many words as they could remember, in any order. When starting the task, each participant was randomly assigned one of the following conditions:

• Case doesn't matter: Under this condition, the instructions given to the participants didn’t mention the case of the words, all words were presented in lowercase, and a word was considered correctly recalled if the spelling was correct, the case of the letters didn’t matter.
• Case matters: Under this condition, the instructions mentioned that the case of the words mattered, each word had a 50% chance of being shown capitalized, that is, with the first letter in uppercase. A word was considered correctly recalled if the spelling and the case of the letters matched the presented word.

Here are the full instructions and word lists that were used. Participants were sourced through Amazon Mechanical Turk (yes, this was in 2013, and Mechanical Turk was still fairly hip).

The data

The task was live on Mechanical Turk between 2013-06-26 and 2013-06-27 and during that time 114 participants completed the Case matters condition and 117 participants the Case doesn't matters condition. The final dataset has one row per participant, with the following columns:

• subject: An anonymized participant identifier.
• condition: The condition the participant ended up with, Case matters or Case doesn't matter.
• presented_wordlist: The word list the participant was presented with.
• answer: The words the participants wrote in the answer box when trying to recall the previously shown words.
• n_correct: How many words the participant correctly recalled. In the Case matters condition only correctly capitalized words count as a correct recall.
• max_correct: The number of shown words, that is, 12.
• submitted_at: The time stamp when the participant submitted the task.
• completion_seconds: How long time it took from when the participant started reading the instructions to when the participant submitted the task.
• subject_comment: An optional free-form comment left by the participant after having completed the task.

A quick analysis

There are many ways one could analyze this data. Here’s a quick one in R that doesn’t consider which word list participants were given, nor how quickly participants completed the task. Let’s start by loading the packages and dataset:

library(tidyverse)
library(brms)
library(bayesplot)

memory_experiment <- read_csv("case-matters-memory-experiment.csv")
select(memory_experiment, subject, condition, n_correct, max_correct)

## # A tibble: 231 × 4
##    subject        condition           n_correct max_correct
##    <chr>          <chr>                   <dbl>       <dbl>
##  1 A1BY04BWSZTFGX Case matters                5          12
##  2 A3NV8GEG3IEEWG Case matters                3          12
##  3 A10MEXRNAC2LV2 Case doesn't matter         6          12
##  4 A3HFWLGG0K527B Case matters                8          12
##  5 ABOEYY9Y0PFRI  Case matters                5          12
##  6 A171DR7TM2I1KD Case matters                5          12
##  7 A1R02UXIIZL1SO Case matters                7          12
##  8 AT0COJ1G23ZB0  Case matters                8          12
##  9 A33RWT46JOG5HR Case doesn't matter         6          12
## 10 A2S5B9FEIJIGGB Case doesn't matter         4          12
## # … with 221 more rows

Let’s take a look at how participant 2 performed:

cat(sep = "\n",
  "Participant 2, Condition: uppercase/lowercase matters",
  paste("Presented wordlist:", memory_experiment$presented_wordlist[2]),
  paste("Answer:", memory_experiment$answer[2]),
  paste("N correctly recalled:", memory_experiment$n_correct[2])
)

## Participant 2, Condition: uppercase/lowercase matters
## Presented wordlist: rifle;desire;Porch;profit;chill;square;Insect;corner;Start;rider;English;asset
## Answer: English;asset;rider;sport;Chill;project
## N correctly recalled: 3

They were given the Case matters condition and were presented with a word list where, on average, 50% of the words were capitalized. Participant 2 only scored 3 on this task, as they incorrectly capitalized chill and wrote the words sport and project which never occurred in the presented word list. Let’s look at how many words participants in the two conditions correctly recalled overall:

memory_experiment |> 
  ggplot(aes(n_correct, fill = condition)) +
  geom_bar() +
  facet_grid(condition ~ .) +
  labs(
    x = "Number of correctly recalled words",
    y = "Number of participants"
  ) +
  theme(legend.position = "none")

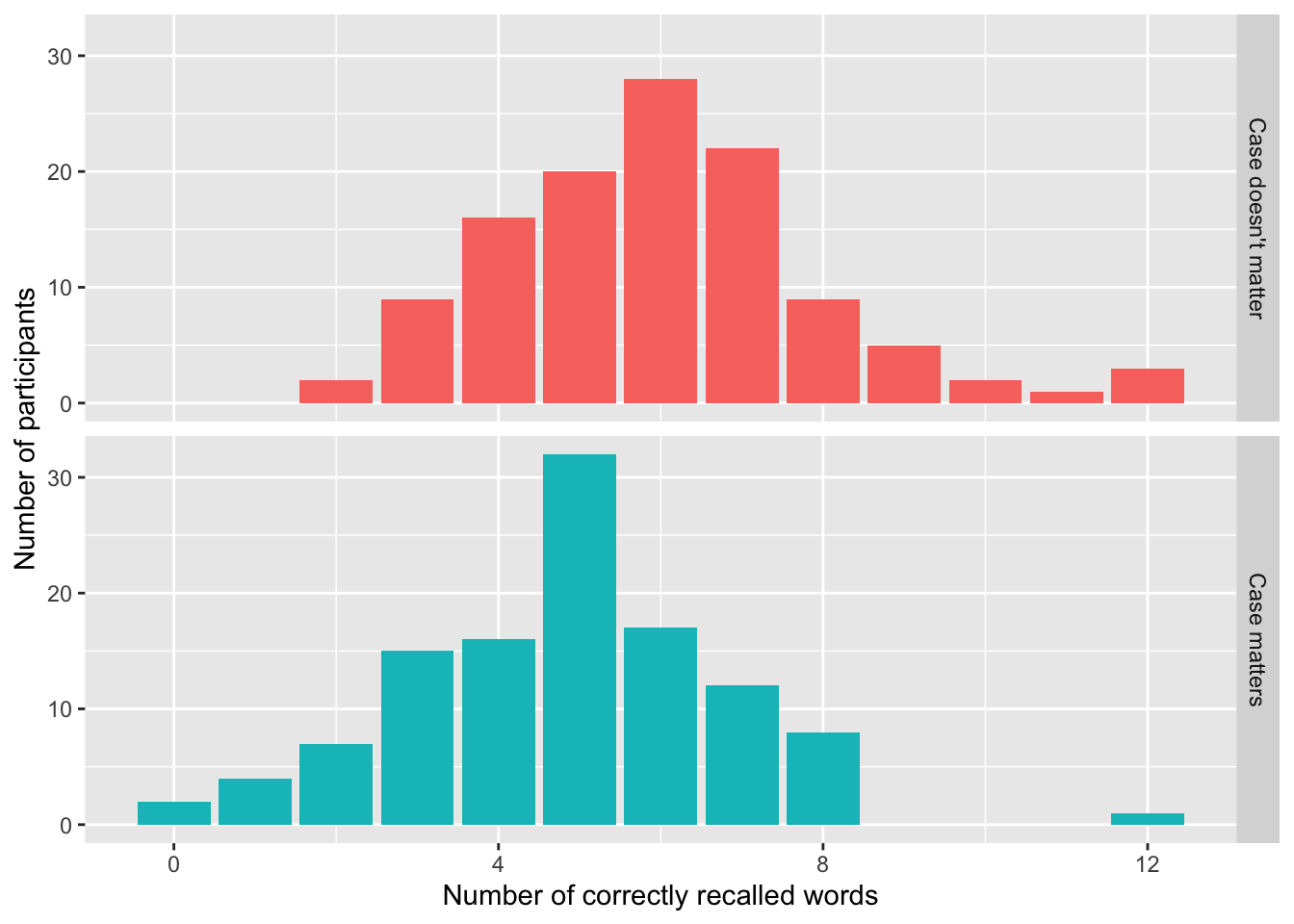
Already here, we can clearly see that it’s harder to correctly recall words if you also have to remember whether they were capitalized or not. And we could probably stop here, but let’s throw in some Bayesian modeling while we’re at it here assuming a hierarchical binomial model using the great brms package. Loosely, this model assumes each participant has a fixed probability to remember each word. Participants’ recall probabilities are then assumed to come from a population level distribution which, under the Case matters condition is shifted according to another population level distribution. Fitting this model, and doing some transforms at the end, will allow us to estimate the posterior population mean number of recalled words in both the Case matters and the Case doesn't matter conditions plus the difference between these two distributions.

# Fitting the model
fit <- brm(
  n_correct | trials(max_correct)  ~ 1 + condition + (1 + condition | subject),
  data = memory_experiment,
  family = binomial(link = logit),
  prior = c(
    # Fairly uninformative priors
    prior(normal(0, 1.5), class = Intercept),
    prior(normal(0, 1.5), class = b),
    prior(normal(0, 1), class = sd)),
  iter = 10000, warmup = 2000, chains = 4, cores = 4
)

# Convering from log-odds to expected number of correct recalls out of 12. 
max_correct <- unique(memory_experiment$max_correct)
posterior_n_correct <- as_draws_df(fit, variable = "^b_", regex = TRUE) |> 
  transmute(
    case_doesnt_matter = plogis(b_Intercept) * max_correct,
    case_matters = plogis(b_Intercept + b_conditionCasematters) * max_correct,
    case_doesnt_matter_improvment = case_doesnt_matter - case_matters
  ) 

# Plotting the posterior distributions
posterior_n_correct_nice_names = rename(posterior_n_correct,
  `Number of correctly recalled words\nwhen case doesn't matter` = case_doesnt_matter,
  `Number of correctly recalled words\nwhen case matters` = case_matters,
  `Improvement in recall\nwhen case doesn't matter` = case_doesnt_matter_improvment
)

mcmc_areas(posterior_n_correct_nice_names) + 
  ggtitle(
    "Posterior population means", 
    "with medians and 80% intervals")

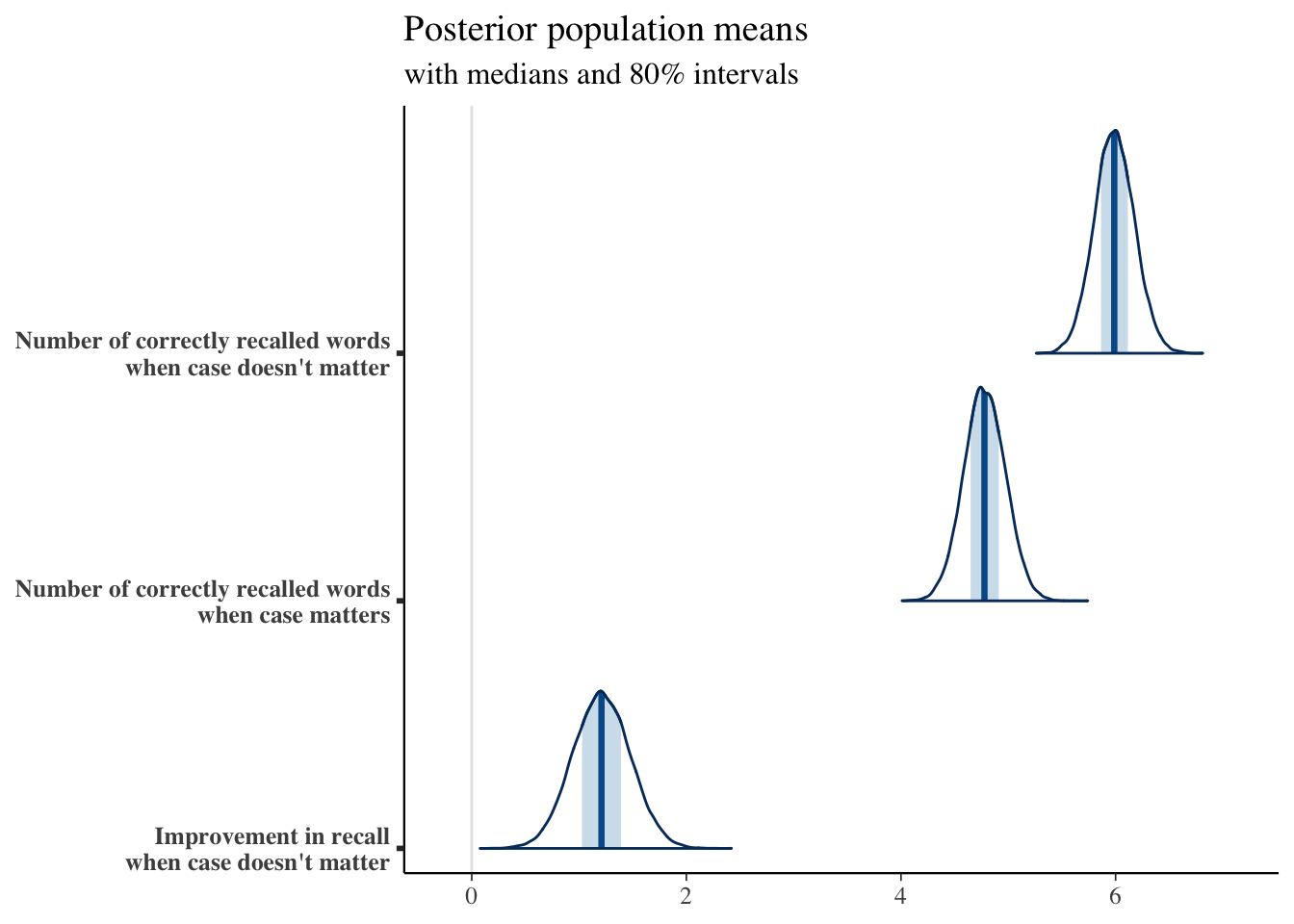
Finally, getting out the posterior medians and 80% uncertainty intervals:

posterior_n_correct |> 
  sapply(quantile, probs = c(0.1, 0.5, 0.9)) |>
  round(2) |> 
  t() 

##                                10%  50%  90%
## case_doesnt_matter            5.75 5.99 6.23
## case_matters                  4.53 4.78 5.03
## case_doesnt_matter_improvment 0.87 1.21 1.55

So in the Case doesn't matter we would expect the average participant to recall 5.99 ± 0.24 words (± here is the 80% uncertainty interval around this estimate) while in the Case matters case the average participant would only correctly recall 4.78 ± 0.25 out of 12 words. That is, the Case matters condition results in an expected 1.21 ± 0.34 improvement in number of words recalled. That is, assuming a population that’s similar to the people hanging out on Mechanical Turk in 2013.